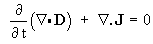2. Obtención de las Ecuaciones de Maxwell para medios en movimiento lento a partir de las Ecuaciones Minimales.

-->

-->

Todo estudioso del electromagnetismo sabe que en la física clásica newtoniana las leyes de la mecánica son invariantes bajo las transformaciones galileanas, pero, en cambio las leyes del electromagnetismo expresadas por las Ecuaciones de Maxwell no lo son. Solo son invariantes dentro del marco de la Teoría de la Relatividad de Einstein, donde los sistemas inerciales están relacionados mediante las ecuaciones de transformación de Lorentz, en lugar de las galileanas. Por lo que seguramente causará sorpresa y hasta incredulidad lo que se demuestra a continuación, en todo caso espero que motive un debate serio al respecto por parte de los interesados.

-->

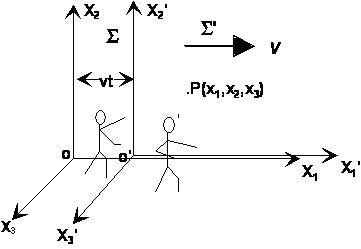
Fig. Sistema de referencia S' que se mueve con la velocidad v respecto al sistema S.

En el caso de un movimiento lento, es decir que la velocidad v con que se mueve el sistema

--> S’ es muy pequeña en comparación con c (c velocidad de la luz) tal que (v/c)² = 0, las ecuaciones de transformación de Lorentz, se reducen a las Galileanas de la Física clásica Newtoniana, las que se escriben a continuación:

A partir de las Ecuaciones Energéticas Minimales, demostraremos que en este caso , no obstante utilizarce las ecuaciones de transformación Galileanas (1), (2), (3), (4), las Ecuaciones de Maxwell conservan su invariancia en sistemas inerciales, es decir formalmente son las mismas en el sistema estacionario S y el sistema en movimiento S’ lo que se ilustra en el cuadro adjunto, pero en cambio el campo electromagnético se transforma.

-->

-->

En el capítulo1 anteriormente publicado en el blog, se utilizaron las Ecuaciones Minimales particularizadas para el caso de un medio en reposo, para obtener las cuatro Ecuaciones de Maxwell, en esta oportunidad partiremos de las Ecuaciones Minimales para un medio o sistema en general en movimiento las que escribimos a continuación:

(5)

(6)

Sustituyendo las correspondientes expresiones energéticas y efectuando las operaciones indicadas en las Ecuaciones Energéticas Minimales anteriores, se obtienen las ecuaciones siguientes:

(7)

(8)

-->

Las componentes del campo electromagnético para el sistema en reposo son funciones de las coordenadas (x₁, x₂, x₃ ) y del tiempo t , lo que expresamos a continuación:

(9)

(10)

Las coordenadas de un punto referidos al sistema S’ en movimiento están relacionados con las correspondientes referidas al sistema S estacionario, por las ecuaciones de Transformación Galileanas (1), (2), (3), y (4). Teniendo en cuenta estas ecuaciones, se obtiene las siguientes expresiones para las derivadas parciales respecto a las mismas:

(11)

(12)

Donde: es el delta de Kronecker.

Como consecuencia de las expresiones (11), (12) se puede comprobar que se cumple la siguiente identidad del operador nabla:

(13)

Tomando la derivada total respecto al tiempo de D_a y B_a , se obtiene:

(14)

(15)

Teniendo en cuenta las expresiones (13), (14), (15), las ecuaciones (7), (8) se pueden escribir en la forma siguiente:

(16)

(17)

A continuación escribimos las ecuaciones (16) para : alfa = 1, 2, 3.

(18)

(19)

(20)

Para que las ecuaciones (18), (19), (20 referidas al sistema en movimiento S’ sean invariantes, es decir, formalmente idénticas a las correspondientes para el sistema estacionario S , de conformidad con el Principio de la invariancia de las Ecuaciones de Maxwell en sistemas inerciales , se deben cumplir las siguiente igualdades:

(21)

(22)

(23)

(24)

(25)

(26)

(27)

(28)

Completando la identificación despejamos H₃ y H₂ de las (26) y (28), y luego las sustituimos en la (18), obteniéndose la siguiente:

(29)

pero, teniendo en cuenta la tercera ecuación de Maxwell:

(30)

la (29) se puede escribir en la forma siguiente:

(31)

donde:

(32)

es la ecuación de transformación de la respectiva componente densidad de corriente.

Las ecuaciones de transformación de las componentes del campo magnético (25), (26), (28), y las (24), (27), (32) de las densidades de corriente, se pueden escribir en las siguientes formas vectoriales:

(33)

(34)

Procediendo en forma similar con la ecuación (17) el interesado podrá comprobar el cumplimiento de la invariancia de la correspondiente Ecuación de Maxwell y se obtiene la siguiente ecuación de transformación del campo eléctrico:

(35)

El interesado podrá comprobar que las ecuaciones de transformación (33), (34) y (35) son idénticas a las que se obtienen cuando se aproximan las correspondientes ecuaciones de transformación relativististas del campo electromagnético y la densidad de corriente (hacer click para visualizar ó bajar archivo PDF ), para el caso de un movimiento lento, es decir: para c >> v y (v/c)² = 0.

1. Obtención de las ECUACIONES DE MAXWELL para medios en reposo a partir de las Ecuaciones Minimales

Las Ecuaciones de Maxwell como síntesis del electromagnetismo clásico pre-relativista fue el resultado de un proceso histórico de trabajos experimentales que condujeron a las leyes empíricas de Coulomb, Ampere, Faraday y Gauss, las cuales, gracias a la genialidad de Maxwell fueron formalizadas matemáticamente y les agregó lo que faltaba - el termino de corriente de desplazamiento - basado en una hipótesis, razón por la cual es muy probable que al interesado le llame la atención y motive especial curiosidad , que se obtengan las Ecuaciones de Maxwell formalmente a partir de otras ecuaciones – las Ecuaciones Minimales – las que escribimos nuevamente a continuación:

Ecuaciones Minimales para un medio en reposo
Para obtener las Ecuaciones de Maxwell a partir de las Ecuaciones Minimales que se han escrito anteriormente, estas deben ser previamente particularizadas para procesos energéticos en sistemas o medios en reposo, por que como se sabe, las cuaciones fueron formuladas por Maxwell presuponiendo la existencia de un medio en reposo -el llamado Eter - en el cual se propagan las ondas electromagnéticas con la velocidad de la luz.Maxwell fue un firme creyente de su existencia.
Teniéndose en cuenta que se puede intercambiar el orden en que se toman las derivadas en los primeros términos de las Ecuaciones Minimales anteriores, las que rescribimos a continuación:


Tanto Ue como Tm son funciones de las componentes del campo eléctrico y magnético respectivamente, pero estas a su ves son funciones de las coordenadas espaciales (x1 , x2 , x3 ) y del tiempo t, por lo tanto también serán funciones de las coordenadas espaciales y del tiempo, es decir:


En el caso de un medio o sistema en reposo las coordenadas espaciales x1, x2, x3 no varían en función del tiempo, por lo que las derivadas totales respecto al tiempo de Ue y Tm son iguales a sus derivadas parciales respecto al tiempo. Luego de intercambiar nuevamente el orden de las derivadas, se obtienen las Ecuaciones Minimales para un sistema o medio en reposo las que escribimos a continuación:
(1)
(2)A partir de las Ecuaciones Minimales (1) y (2) procederemos a obtener las Ecuaciones de Maxwell, para lo cual utilizaremos las conocidas expresiones energéticas:
(3)expresa la densidad de energía eléctrica almacenada por unidad de volumen.

(4)expresa la densidad de energía magnética almacenada por unidad de volumen.

(5)expresa la función densidad disipación
.
(6)expresa la potencia suministrada por unidad de volumen.
Debe tenerse presente que las componentes Eα y Hα del campo eléctrico y magnético,desde el punto de vista matemático son variables de estado o coordenadas generalizadas.
Efectuando las derivadas parciales de las expresiones (3), (5) y (6) indicadas en las Ecuaciones Minimales (1) se obtiene lo siguiente:

(7)
(8)

(9)
Sustituyendo (7), (8) y (9) en (1) se obtiene la siguiente:

(10)Utilizando una conocida identidad se tiene para el segundo miembro de (10)

(11)Sustituyendo (11) en el segundo miembro de la ecuación (10), la misma se puede escribir en la forma siguiente:

(12).las que se pueden escribir en la siguiente en la forma vectorial equivalente:

(13)o en función del vector desplazamiento y la densidad de corriente J = g E :

(14)Que es la Ecuación de Maxwell que expresa la Ley de Ampere Generalizada.

Procediendo en forma similar con las Ecuaciones Minimales (2), el interesado podrá comprobar que se obtiene la siguiente ecuación :

(15) que es precisamente la Ecuación de Maxwell que expresa la Ley de inducción de Faraday.

En forma similar se pueden obtener las Ecuaciones de Maxwell restantes que expresan la Ley de Gauss eléctrica y magnética, teniéndose en cuenta además el Principio de Conservación de la Carga expresado por la ecuación de continuidad, la que escribimos a continuación en su forma diferencial para la carga eléctrica:

(16)Tomamos la derivada parcial a cada miembro de las ecuaciones de equilibrio (10) con respecto a las coordenadas xa , y teniendo en cuenta una conocida identidad se obtiene la siguiente ecuación:

(17)
Para: alfa = 1,2,3

Sumando las ecuaciones (17) y luego de factorizar términos se obtiene:

(18)
La que se puede escribir en la forma siguiente:

(19)Recordando que la ecuación (19) se reduce a la siguiente:

(20) Puesto que la ecuación (20) debe ser consistente con la ecuación de continuidad (16), se deduce, que debe cumplirse:

(21)que es la tercera Ecuación de Maxwell que expresa la Ley de Gauss eléctrica.
Procediendo en forma similar, el interesado podrá obtener la cuarta Ecuación de Maxwell siguiente:

(22)
CONCLUSIONES